Newton-Raphson Method in Python

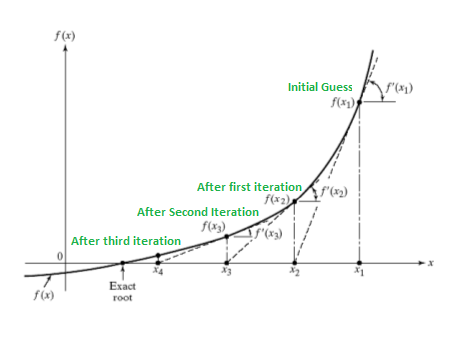
The Newton-Raphson Method is a simple algorithm to find an approximate solution for the root of a real-valued function \(f(x)=0\). If the function \(f\) satisfies sufficient assumptions then after repeative steps the \(x_{n+1}\):

\(x_{n+1} = x_n – \frac{f(x_n)}{f'(x_n)}\)

will be a good approximation to the root.

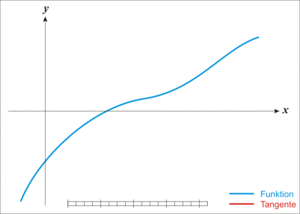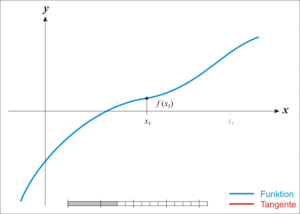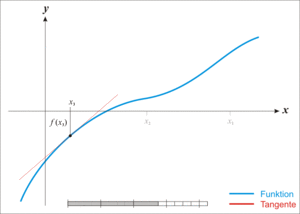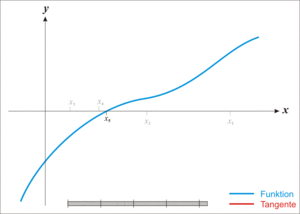
Failure of the method to converge to the root

It is important to review the proof of quadratic convergence of Newton’s method before implementing it. Specifically, one should review the assumptions made in the proof. For situations where the method fails to converge, it is because the assumptions made in this proof are not met.

Calculate Derivatives in Python

The Newton-Raphson Method requires to calculate the first derivative of the function \(f\). This can be done with the SymPy library. Let’s provide an example by funding the first derivative of the function \(f(x) = x^2-4 \times x-5\)

import numpy as np
from sympy import *

# define what is the variable
x = symbols('x')

# define the function
f = x**2-4*x-5

# find the first derivative
fderivative = f.diff(x)
fderivative
 

2x-4

# get a valua of the derivate for a specific x
# let's say f'(0)

fderivative.evalf(subs= {x:0})
 

-4

Newton-Raphson Method

Since we calculate defined the function \(f(x)\) and the derivative \(f'(x)\) we are in a position to apply the simple Newton-Raphson Method.

We will start with \(x_0=1\):

xn = 1
for i in range(10):
    xn = xn - np.float(f.evalf(subs= {x:xn})) / np.float(fderivative.evalf(subs= {x:xn}))
    print(f'The {i+1} iteration xn is {xn:.2} and f(xn) is {np.float(f.evalf(subs= {x:xn})):.2}')
  

The 1 iteration xn is -3.0 and f(xn) is 1.6e+01
The 2 iteration xn is -1.4 and f(xn) is 2.6
The 3 iteration xn is -1.0 and f(xn) is 0.14
The 4 iteration xn is -1.0 and f(xn) is 0.00055
The 5 iteration xn is -1.0 and f(xn) is 8.4e-09
The 6 iteration xn is -1.0 and f(xn) is 9.5e-125
The 7 iteration xn is -1.0 and f(xn) is 9.5e-125
The 8 iteration xn is -1.0 and f(xn) is 9.5e-125
The 9 iteration xn is -1.0 and f(xn) is 9.5e-125
The 10 iteration xn is -1.0 and f(xn) is 9.5e-125

As we can see at the third iteration it found an approximate solution which is correct since \(f(-1) = 0\).

Issues with the Newton-Raphson Solutions

The algorithm found a solution but it does not mean that this solution is unique. Actually it found the closest one. Let’s see what we would get if we had chosen as a starting point the \(x_0=10\)

xn = 10
for i in range(10):
    xn = xn - np.float(f.evalf(subs= {x:xn})) / np.float(fderivative.evalf(subs= {x:xn}))
    print(f'The {i+1} iteration xn is {xn:.2} and f(xn) is {np.float(f.evalf(subs= {x:xn})):.2}')
  

The 1 iteration xn is 6.6 and f(xn) is 1.2e+01
The 2 iteration xn is 5.3 and f(xn) is 1.7
The 3 iteration xn is 5.0 and f(xn) is 0.066
The 4 iteration xn is 5.0 and f(xn) is 0.00012
The 5 iteration xn is 5.0 and f(xn) is 4e-10
The 6 iteration xn is 5.0 and f(xn) is 3.8e-124
The 7 iteration xn is 5.0 and f(xn) is 3.8e-124
The 8 iteration xn is 5.0 and f(xn) is 3.8e-124
The 9 iteration xn is 5.0 and f(xn) is 3.8e-124
The 10 iteration xn is 5.0 and f(xn) is 3.8e-124

As we can see at the third iteration it found the other approximate solution which is correct since \(f(5) = 0\).

More Data Science Hacks?

You can follow us on Medium for more Data Science Hacks