Monte Carlo Integration in Python

We will provide examples of how you solve integrals numerically in Python. Let’s recall from statistics that the mean value can be calculated as.

\( E(X) = \frac{1}{b-a} \int_{a}^{b}f(x)dx\)

\((b-a) E(X) = \int_{a}^{b} f(x) dx\)

\((b-a)\frac{1} {N}\sum_{i}f(x_i) \approx \int_{a}^{b}f(x)dx \)

This implies that we can find an approximation of an interval by calculating the average value times the range that we integrate.

Example of Monte Carlo Integration

Let’s say that we want to calculate the following integral where from WolframAlpha we get the solution:

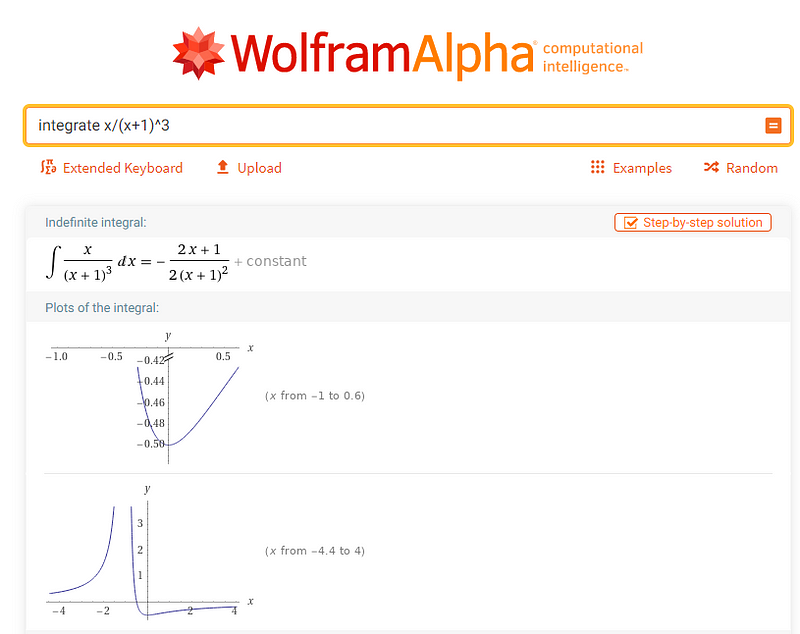
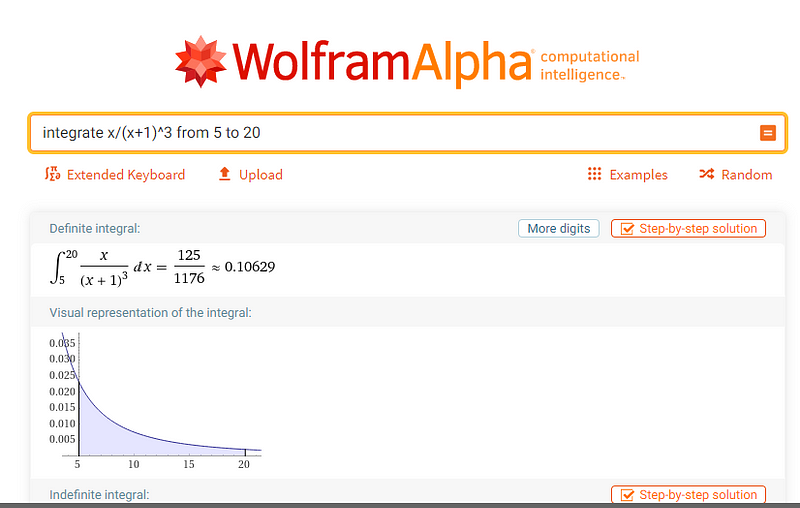
\(\int_{5}^{20}\frac{x}{(x+1)^3}dx = \frac{125}{1176}\approx 0.10629\)

Solution with Python

Let’s see how we can approximate the solution of the finite integral in Python by applying the Monte Carlo Integration. The idea is to generate many random values within the range of integration (in our case 10M observations within [5,10]) and then to take the average value divided by the range. This is what we proved at the beginning.

import numpy as np
Ν = 100000000
a = 5
b = 20
x = np.random.uniform(a,b,Ν)

f_x = x/((1+x)**3)

print(np.mean(f_x)*(b-a))

0.10629043477066367

Not bad! The Monte Carlo Integration returned a very good approximation (0.10629 vs 0.1062904)! As we can see, when we face difficulties to solve a finite integral we can approximate it by applying the Monte Carlo Integration Method.