Applications of Poisson Distribution

The Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space if these events occur with a known constant rate and independently of the time since the last event.

---

---

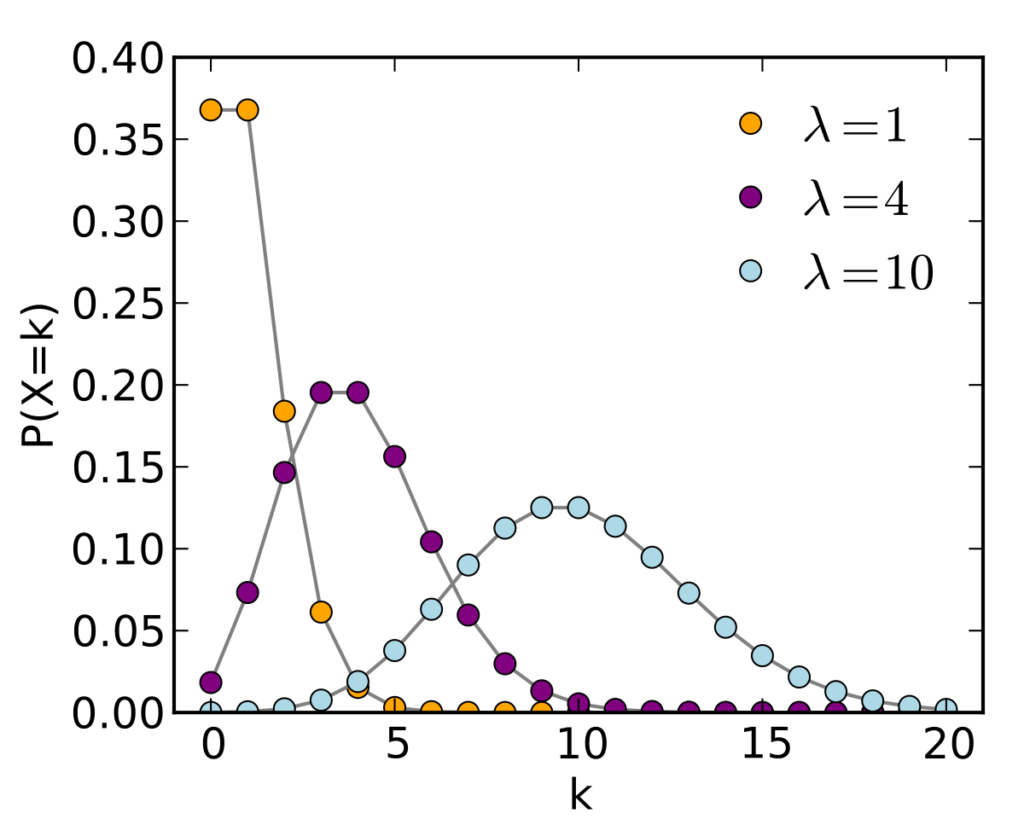
Its Probability Mass Function is: \(P(X=k)=\frac{\lambda^k e^{-\lambda}}{k! }\) where \(\kappa \in \{0,1,2,…\}\) and \(\lambda\) is the average number of events in the interval and is also called event rate.

The Poisson random variable satisfies the following conditions:

1. The number of successes in two disjoint time intervals is independent.
2. The probability of a success during a small time interval is proportional to the entire length of the time interval.

Applications of Poisson Distribution

• the number of deaths by horse kicking in the Prussian army (first application)
• birth defects and genetic mutations
• rare diseases (like Leukemia, but not AIDS because it is infectious and so not independent) – especially in legal cases
• car accidents
• traffic flow and ideal gap distance
• number of typing errors on a page
• hairs found in McDonald’s hamburgers
• spread of an endangered animal in Africa
• failure of a machine in one month
• number of goals in a tournament
• number of meteorites greater than 1 meter diameter that strike Earth in a year
• number of patients arriving in an emergency room between 10 and 11 pm

Example 1:

Jane makes on average 1 mistake per 2 pages when she types. What is the probability to complete 4 pages without making any mistake?

Solution

In this case the \(\lambda = \frac{4}{2} \times 1 =2 \) and we want the \(P(X=0) = \frac{2^0 e^{-2}}{0!} = 13.53\% \)

---

Example 2:

The average number of goals in a World Cup soccer match is approximately 2.5. What is the probability to score less than two goals in a match?

Solution

The \(\lambda = 2.5 \) and we want: \(P(X<2) = P(X=0)+P(X=1) = e^{-2.5}+2.5e^{-2.5}=0.082+0.205=0.287=28.7\%\)

---

Example 3:

If electricity power failures occur with an average of 3 failures every twenty weeks, calculate the probability that there will not be more than one failure during a particular week.

Solution

The \(\lambda = 3/20=0.15 \) and we want: \(P(X \leq 1) = P(X=0)+P(X=1) = e^{-0.15}+0.15e^{-0.15} = 0.9898 = 98.98\%\)

Note: In another post we provided an example of Exponential Distribution!