Market Basket Analysis and Association Rules from Scratch

We have provided a tutorial of Market Basket Analysis in Python working with the mlxtend library. Today, we will provide an example of how you can get the association rules from scratch. Let’s recall the 3 most common association rules:

Association Rules

Given a set of transactions, find rules that will predict the occurrence of an item based on the occurrences of other items in the transaction. For example, we can extract information on purchasing behavior like “If someone buys beer and sausage, then is likely to buy mustard with high probability“

Let’s define the main Associaton Rules:

Support

It calculates how often the product is purchased and is given by the formula:

\(Support(X) = \frac{Frequency(X)}{N (\#of \;Transactions)}\)

\(Support(X \rightarrow Y) = \frac{Frequency(X \bigcap Y)}{N (\#of \;Transactions)}\)

Confidence

It measures how often items in Y appear in transactions that contain X and is given by the formula.

\(Confidence(X \rightarrow Y ) = \frac{ Support(X \rightarrow Y )}{ Support(X) }\)

Lift

It is the value that tells us how likely item Y is bought together with item X. Values greater than one indicate that the items are likely to be purchased together. It tells us how much better a rule is at predicting the result than just assuming the result in the first place. When lift > 1 then the rule is better at predicting the result than guessing. When lift < 1, the rule is doing worse than informed guessing. It can be given by the formula:

\(Lift(X \rightarrow Y ) = \frac{ Support(X \rightarrow Y )}{ Support(X)\times Support(Y) }\)

Coding Part

By 2 Products

Assume that we are dealing with the following groceries.xlsx file:

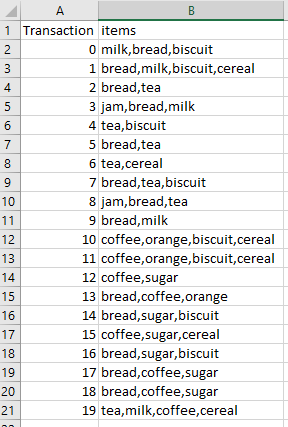
We want to transform the data into order id and product id.

import pandas as pd

df = pd.read_excel("groceries.xlsx")
df['items'] = df['items'].apply(lambda x: x.split(","))

df = df.explode('items')
df.columns = ['oid', 'pid']
df.reset_index(drop=True, inplace=True)

df

Write the function which returns the three association rules such as support, confidence and lift for every possible pair. The my_pid is the antecedent and the y is the consequent.

def all_x_y(df, my_pid, y):
    df = df.copy()
    N = len(df.oid.unique())
    
    tmp = pd.DataFrame({'XY':[my_pid,y]})
    tmp = df.merge(tmp, how='inner', left_on='pid', right_on='XY' )
    
    numerator = sum(tmp.groupby('oid').size()==2)/N
    a = len(df.loc[df.pid==my_pid].oid.unique())/N
    b = len(df.loc[df.pid==y].oid.unique())/N
    denominator = a * b
    
        
    lift = numerator/denominator
    confidence = numerator/a
    support = numerator
    
    return (support, confidence, lift)

Let’s see some examples by considering the (milk, bread) and (orange, coffee):

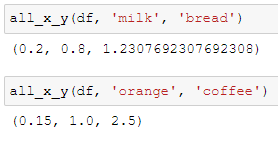
You can confirm that we get the same results with that from the mlxtend module:

onehot = df.pivot_table(index='oid', columns='pid', aggfunc=len, fill_value=0)
onehot = onehot>0

from mlxtend.frequent_patterns import association_rules, apriori

# compute frequent items using the Apriori algorithm
frequent_itemsets = apriori(onehot, min_support = 0.01, max_len = 2, use_colnames=True)

# compute all association rules for frequent_itemsets
rules = association_rules(frequent_itemsets, min_threshold=0.01)
rules
 

Now, let’s see how we can get all the possible pairs.

unique_products = df.pid.unique()
output = []

for i in unique_products:
    for j in unique_products:
        if (i!=j):
            tmp = all_x_y(df, i, j)
            output.append({
                'antecedents':i,
                'consequents':j,
                'support':tmp[0],
                'confidence':tmp[1],
                'lift':tmp[2]
                          })

output = pd.DataFrame(output)
output

By 3 Products

The Market Basket Analysis and the Association rules are becoming more complicated when we examine more combinations. Let’s say that we want to get all the association rules when the antecedents are 2 and the consequent is 1. I.e we have already two items in the basket, what are the association rules of the extra item. The first thing that we will need to do is to generate all the possible combinations by 3 (or even by 2, and then add the right-hand side). For example:

x = list(itertools.combinations(unique_products, 3))
x

In another tutorial, we will show you how you can generate the association rules for more than two items. Stay tuned!