KENO: Highway Robbery

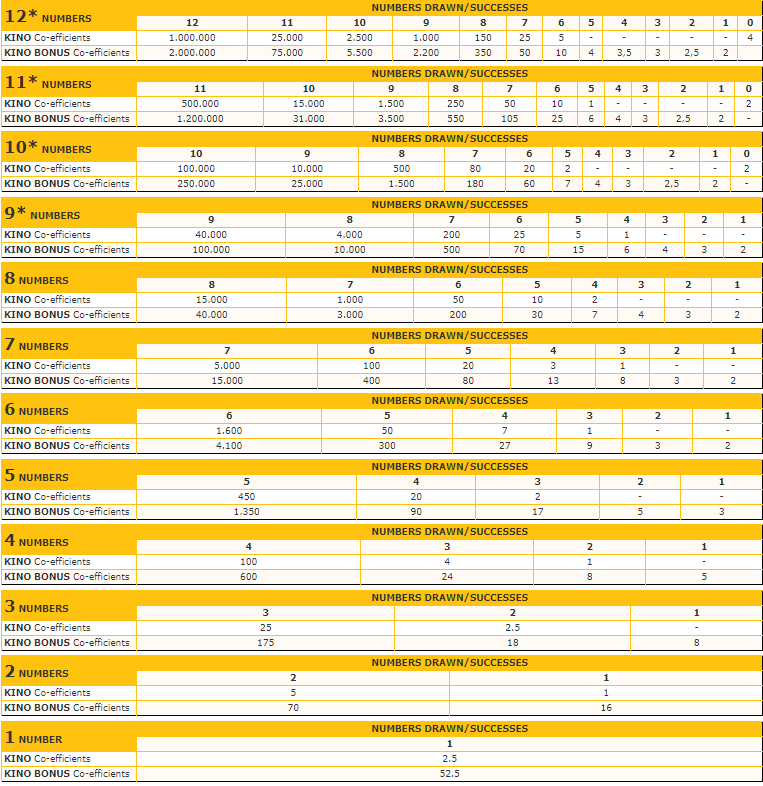
Keno is a popular lotter-like gambling game where there are 80 numbers (from 1 to 80) and in every draw it returns 20 numbers out of 80. The player can choose how many numbers would like to play, usually it is from 1 to 12 unique numbers. Every lottery/casino defines its own pay-off. We will discuss about OPAP’s pay-off which can be found here, or for convenience at the image below:

---

---

Expected Return Formula

The Expected Value is the expected return of a discrete distribution.

Let \(X\) be a random variable with a finite number of finite outcomes \(x_1,x_2,…,x_k\) occurring with probabilities \(p_1, p_2,…,p_k\), respectively. The expectation of \(X\) is defined as:

\(E[X]= \sum_{i=1}^{k}x_ip_i\)

Thus, in our case we need to find the probability of each number to be drawn and its corresponding pay-off. The successes (i.e. the drawn numbers) follow the Hypergeometric distribution which is:

\(Pr(X=k) = \frac{ {K \choose k} {N-K \choose n-k} }{ {N \choose n} }\)

where:

• \(N\) is the population size, in our case 80.
• \(K\) is the number of success states in the population, in our case 20.
• \(n\) is the number of draws.
• \(k\) is the number of observed successes.

Google Spreadsheets have the build-in function of calculating the Hypergeometric distribution which is the HYPGEOM.DIST(num_successes, num_draws, successes_in_pop, pop_size) . We have created a Google Spreadsheet here which estimates the Expected Return as well as the Variance for all Keno games (i.e. from choosing 1 number up to 12 numbers). You can go through this example and you can use it as a starting point for other similar lottery problems.

Expected Return per Keno Game

The table below represents the expected return for each Keno game plus the variance assuming that the player bets 1$.

Numbers Played	Return	Variance
1	0.6250	1.17
2	0.6804	1.42
3	0.6938	9.06
4	0.6920	31.06
5	0.6999	135.28
6	0.6907	338.99
7	0.6996	621.00
8	0.6900	1,145.83
9	0.6978	1,708.01
10	0.6931	1,782.85
11	0.6912	4,345.94
12	0.6978	2,352.80

---

Q: How much I will make in Keno?

For every 1$ that you play, it is expected to get back around 0.7$, in other words it is expecting to LOSE 30% of your money. Then, why people keep playing this game? This is a difficult question to be answered, and there is no unique answer since every player has his\her own reasons, but we have to keep in mind that people have different utility functions. So, the key part in the pay-off is the variance which shows how volatile is the pay-off which means that even with 1$ there is a chance to make a significant amount of money!

NB: The returns we represented above were before taxes. In Greece, the taxation is 15% for profits from 100€ to 500€ and 20% for any profit amount above 500€!

Just FYI, the probability to get 12 out of 12 correct numbers in Keno, is 1 over 478,261,833 which is less likely than the probability of the mankind to disappear within the next few years!

PS: Still I cannot explain people who play just one number! The probability to win is 1 out of 4 and the pay-off is 2.5 times!!! What is the point to enter a game where it is expected to lose 37% of your money for having the chance to get back just 2.5 times your money! It is much better to go to the casino to play roulette…